Quadrotor Control: State-Space Model
I covered, “PID” (Proportional-Integral-Differential) or, “classical” controller designs for the quadrotor platform in a post last fall…time flies! We really only employ the P and the D elements. The, ‘D’ is the, “lead compensator”. The proportional gain P is the last step and you can see how this design technique is performed in that post.
This is a fine method and I’m guessing it is the extent of the controller design for most quadrotor platforms you buy, and code bases you might use if you buy a controller unit like a Pixhawk and run Ardupilot on it. An old colleague of mine is a leader on Ardupilot project. He walked me through the code a few months ago.
If I were anxious to fly I’d be pulling parts together and droning around my neighborhood with the Pixhawk, an off-the-shelf quadcopter, and Arupilot all tuned-up as they have designed a user-friendly set of tools: PID tuning, etc. I could implement my controller based on my recent lead compensator design.
A lead compensator design (“PID tuned”) in Ardupilot will get me a stable quad. I want to push on to the challenge Bouabdallah presents in his paper: control of the platform over a wider, “flight envelope”. This means when we can’t ignore the gyroscopic effects of the rigid body in particular, and perhaps the propellers. In this case we can’t simplify the equations into a friendly transfer function and use, “classical” design techniques. We need to use, “state-space” techniques.
State-Space Design Techniques
A tendency here is to just form some matrices instead of transfer functions, assume full-state feedback or implement an, “observer”, and use Matlab commands to calculate some gains. We could do that, and it’s what you do in a control systems class quite often.
I never got deeply engaged in the technique largely because it is perhaps overkill for many practical designs for land vehicles and industrial process control. I learned the design steps, but I took a lot of the math for granted as I used Matlab. I never studied or pursued multi-axis, multi-input control design for aircraft and such. Even there often times good modelling and design simplification can get you to transfer functions and classical design methods.
Blakelock’s book provides many examples of classical design to aircraft and missile control problems. “State-Space” techniques have also been coined with the term, “modern” which implies the old tried-and-true classical methods are old-fashioned, but this is a misnomer. The best solution for any problem is the simplest model you can form, and the method you are most comfortable with to achieve confidence in the results that meet your requirements.
In Bouabdallah’s paper we see a reason for state-space design when we don’t ignore body moment-of-inertia and propeller gyroscopic effects. We model the system we’ll successively linearize instead of a transfer function that’s valid near a hovering, horizontal state.
We’re going to attempt controller design that we might use to track a moving target. We’re building a bird of prey to hunt on-the-wing, not just a bird that wants to hover around looking for a mouse! Let’s do this with a drive for deep understanding though, and not just jump to Matlab’s, “LQR” command for some gains we used other geniuses’ math to calculate. I won’t approach their level of genius, but I want to learn as much as I can so here we go…
Platform Sketch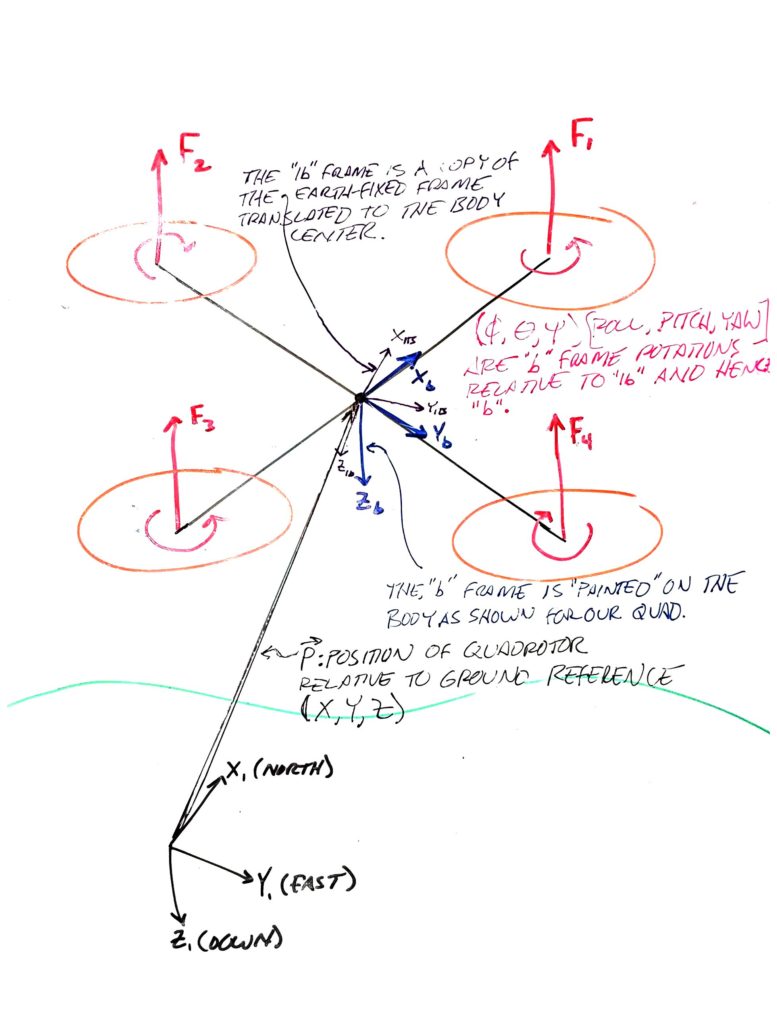
Equations of Motion, Revisited
Refer to an earlier post to review how body moment-of-inertia term appears in the equations of motion for the platform
Propeller Gyroscopic Effect
Refer to an earlier post to see how this term is derived.
Propeller Thrust Inputs
Refer to an earlier post for details.
Quadrotor State Model
The following model copies the Bouabdallah paper. It took some time and effort to arrive at his model through our step-by-step derivations and learning. In the process we clarified through detailed rationale some assumptions in the paper, and comparison will indicate we’ve fixed a few typos relative to the paper.
Up Next…
“Linear Quadratic Methods”: throughout the, “flight envelope” of roll- and pitch-rates that are needed for the, ‘A’ and, ‘B’ matrices. We’ll need a, “control law”. That is, we’ll need a feedback gain matrix to either..
- Regulate to, “zero” state values (steady, horizontal).
- This means we’ll implement a, “Linear Quadratic Regulator” (LQR).
- “Track” to a desired platform attitude, away from horizontal
- This is a linear tracking problem…a twist on the LQR problem.
We’ll cover regulation of states to zero state first, then we’ll cover the tracking problem involving reference inputs. The next post will get into these details!